Projects
The Data Science Center for Smart Industry acts as an advanced data analytics hub for industry, aiming to improve operational efficiency, product quality, innovation and sustainability through the application of data science and analytics techniques of data in industrial processes. Contact with industries will be mediated by SENAI and operationalized through workshops and thematic meetings held between application sectors and CDII researchers. In addition, CDII should act strongly in HR training in Data Science through courses offered by UNICAMP, USP, UNESP, SENAI and AI2. (AU)
The focus of this proposal is the transfer of mathematical knowledge to other areas of science, technology and industry, through a structured research center specially tailored for this purpose. All mathematical knowledge is ultimately applicable, if not directly, through other areas of knowledge. In some areas the application of mathematics is almost immediate. However, the practical implementation of such applicability is often hindered by ingrained incorrect traditions, misdirected scholarship and operational difficulties. In recent years, the growth of science in Brazil, and mathematics in particular, has been remarkable. However, the application of technology, often measured by patents, has not had the same success. To close this gap it is necessary to create institutional structures to establish bridges between the mathematical sciences and applications as a goal in itself. It is not just to guide the theoretical work to areas "potentially relevant" but to take applications to the last consequences, i.e., its effective implementation in the industry at large. One can no longer say that the application can be left to someone else. It is, in fact, a problem concerning all the community and reflects the necessary commitment of pure and applied science with the material and spiritual progress of society. The strategy of this project involves, first, the clustering of imp01iant groups in the areas of applied mathematics at the State of São Paulo and directing their work towards effective applications. The selected groups have demonstrated excellence in the scientific standard in the first place and in many cases, also in relevant applications. In the proposed CEPID participating groups will continue with their usual scientific activities, and at the same time, develop "technology transfer activities" according to the following: 1) master's and doctoral theses necessarily linked with applications in a broad sense, with co-supervision from experts in the applications sectors; 2) conduct at least an annual Transfer Workshop, with participating members of CEPID and representatives of industry, administration, services, educational and technological sectors; 3) regular visits by members of CEPID to institutions with potential for significant applications; 4) development of an online publication called in principle "Technology Transference Experiences" aiming at the consolidation of a more permanent publication. (AU)
Mathematical models allow scientists to translate the behavior of complex systems into a set of equations that describe the relationship between the most important variables. Among the different mathematical models, differential equations constitute a powerful tool for modeling the evolution of systems over time, making them suitable for modeling dynamic phenomena such as population growth, the spread of diseases and the flow of fluids. Typically, the derivation of differential equations that describe a specific phenomenon is done from first principles. However, this can be a challenging task for nonlinear and multiscale phenomena. Recent advances in Machine Learning have motivated several attempts to automate the discovery of differential equations directly from available data about the system. A very promising data-driven approach is Sparse Identification of Nonlinear Dynamics (SINDy), developed by Brunton et al (2016). Assuming that a given phenomenon can be described by a system of differential equations defined by an unknown mapping, SINDy attempts to find this mapping as a linear combination of a finite number of candidate nonlinear functions. The coefficients of this linear combination are calculated by minimizing a loss function formed by a data fidelity term and a regularization term that promotes dispersion. Despite its success in several cases, the basic SINDy formulation described has two difficulties. First, it uses the Euclidean norm in the data fidelity term, which is problematic for real-world data sets corrupted by noise and outliers. Secondly, SINDy requires complete data on all state variables of the system under study, which are not always available. In the present project we will attack these two issues by proposing alternatives to the optimization problem by which the differential equation is identified. The objective is to make SINDy more robust to noise and outliers in the data, and also to expand its applicability to systems with incomplete data on state variables. (AU)
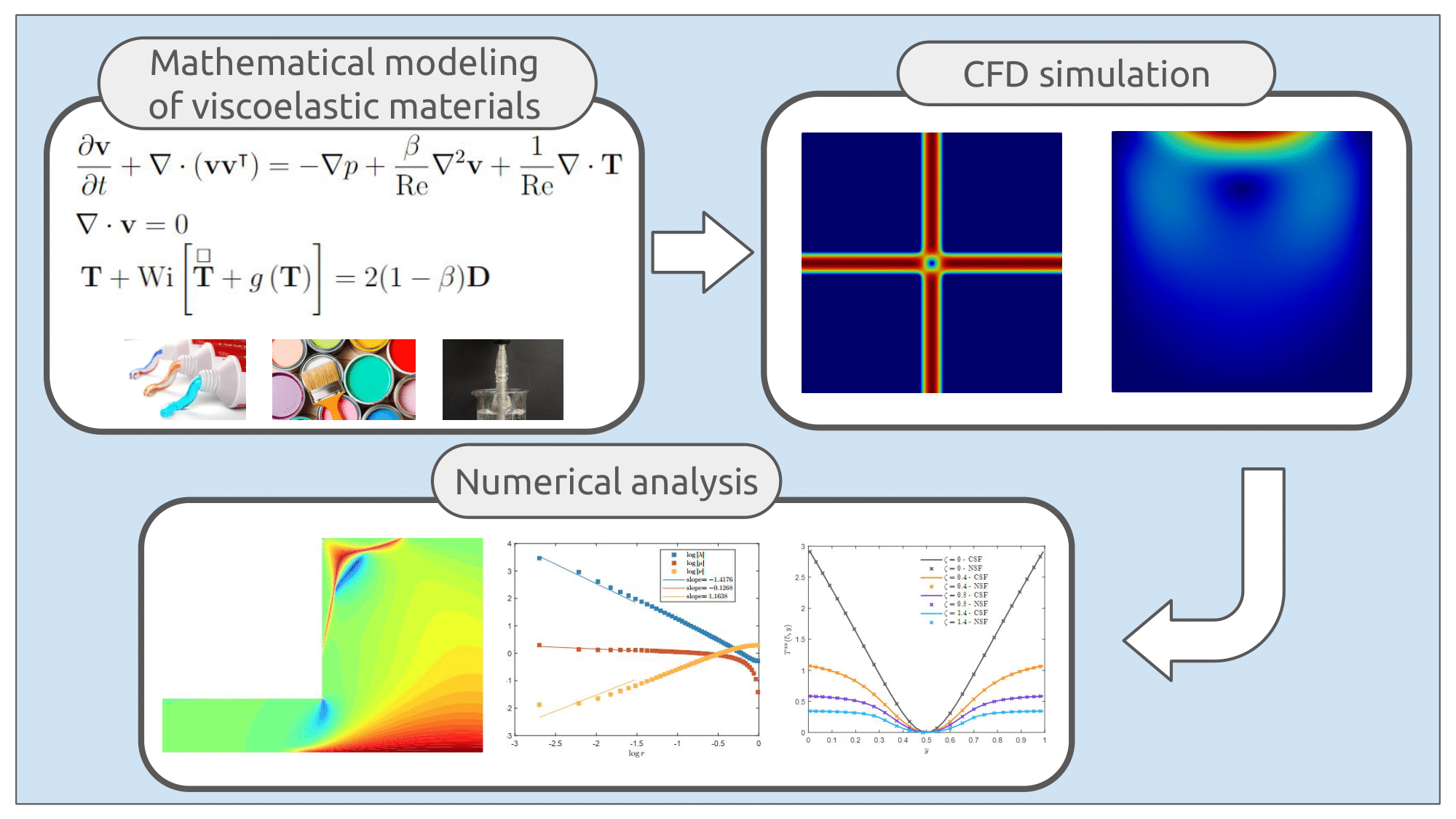
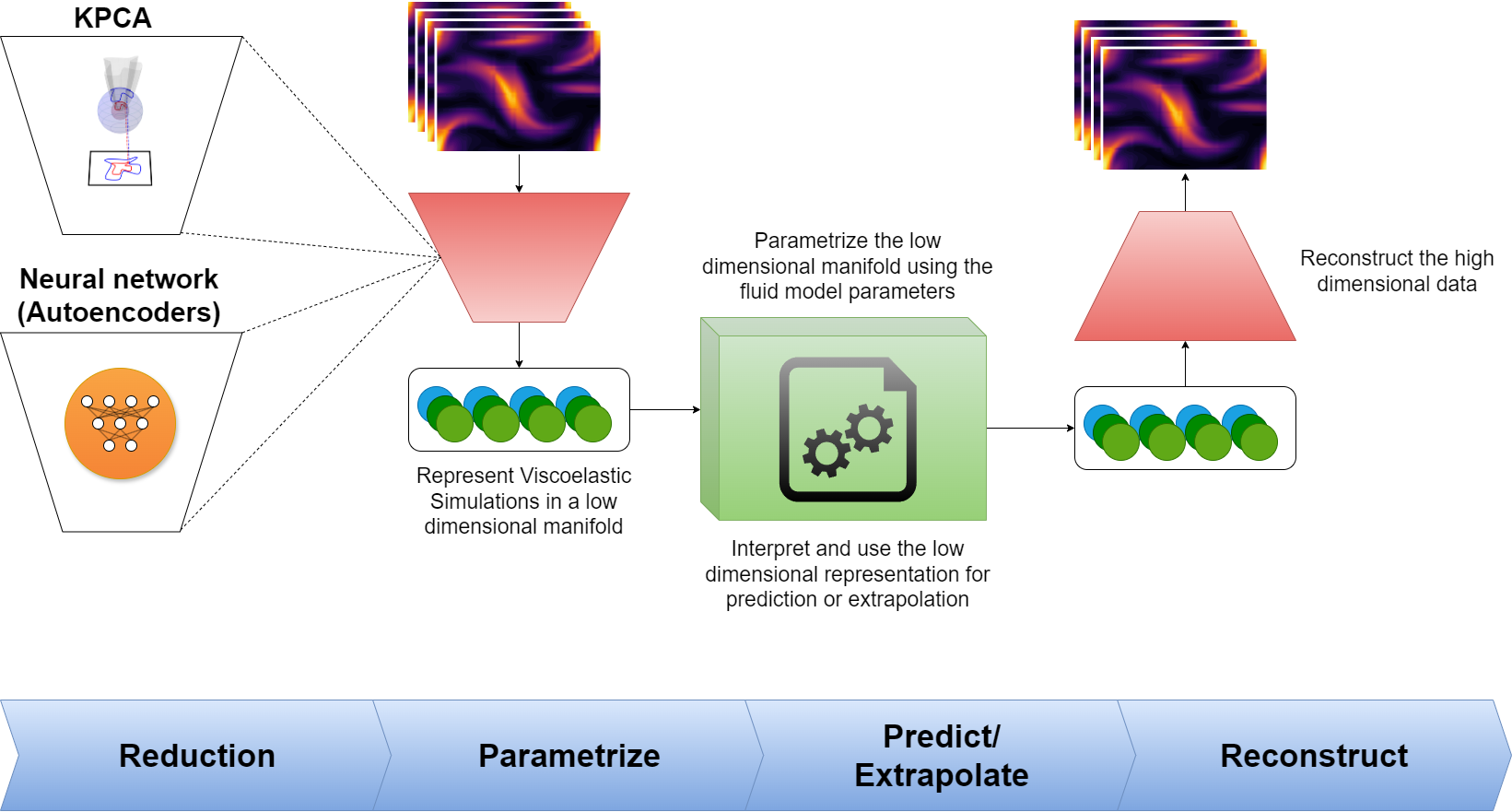
This proposal aims to explore data-driven modeling and machine learning for Computational Fluid Dynamics (CFD), in particular, non-Newtonian and multiphase flows. The main objective is to improve the accuracy, stability and efficiency of numerical methods for simulating complex flows of complex fluids. The project will use simulation data to investigate reduced-order sparse modeling and learning algorithms, while addressing challenges such as convergence analysis and interpretability of Artificial Intelligence-driven methods. The ultimate goal is to reduce computational costs and improve predictions of nonlinear dynamic systems found in applications of biological fluids, droplet impact, gas bubble interaction, among others. This area of research in which this project is inserted is full of exciting possibilities, offering countless open problems and great challenges to be explored and addressed...
Data sciences, technological solutions and computer simulations.
Publications
1. Rafael A. Figueiredo, Cassio M. Oishi, Fernando T. Pinho and Roney L. Thompson, "On more insightful dimensionless numbers for computational viscoelastic rheology", Journal of Non-Newtonian Fluid Mechanics, 2024.
DOI: 10.1016/j.jnnfm.2024.105282
2. Samuel E. Otto, Cassio M. Oishi, Fabio Amaral, Steven L. Brunton and J. Nathan Kutz, "Machine learning in viscoelastic fluids via energy-based kernel embedding", Journal of Computational Physics, 2024.
DOI: 10.1016/j.jcp.2024.113371
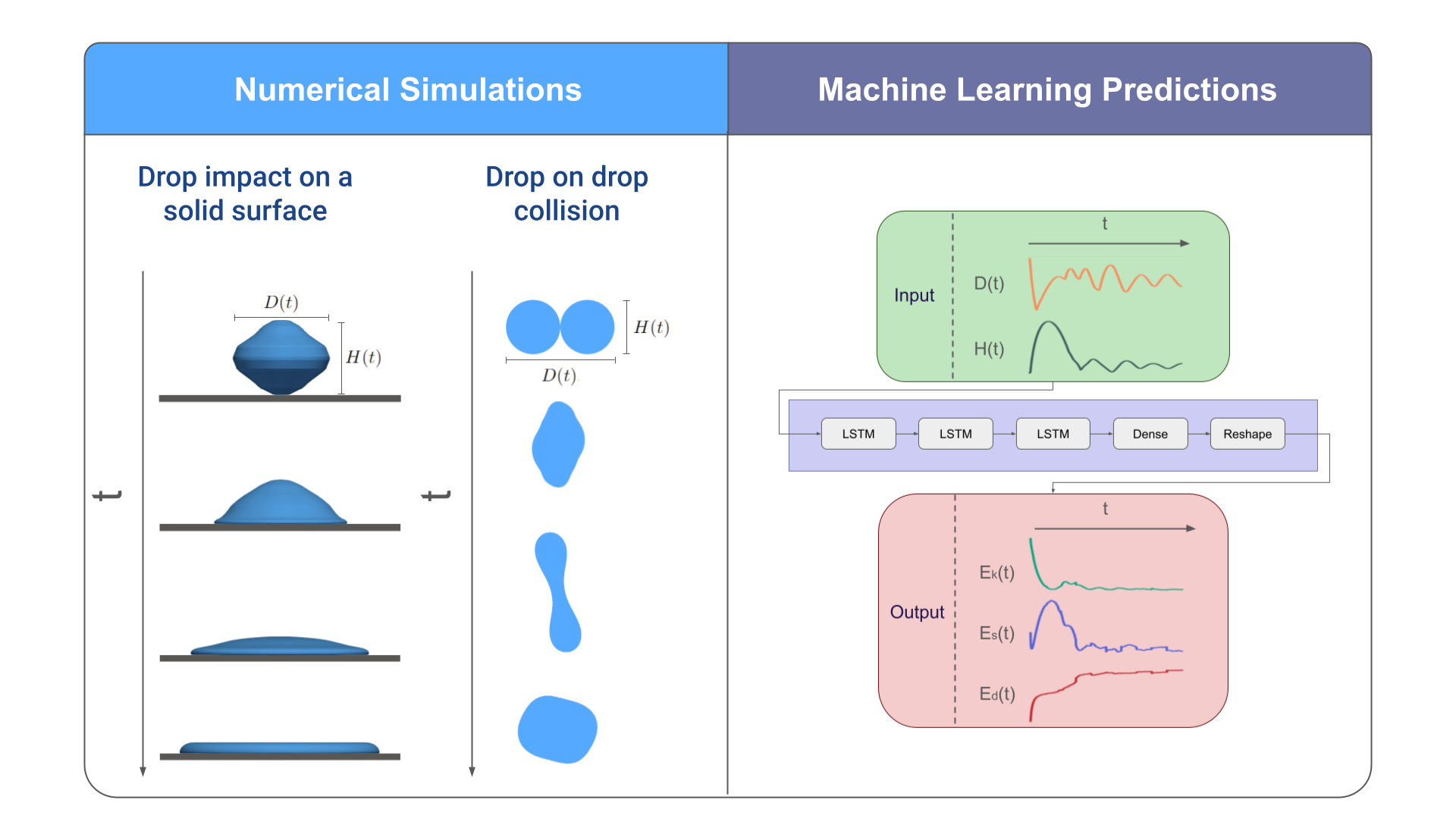
3. Diego A. de Aguiar, Hugo L. França and Cassio M. Oishi, "Predicting Energy Budgets in Droplet Dynamics: A Recurrent Neural Network Approach". International Journal for Numerical Methods in Fluids, 2025.
DOI: 10.1002/fld.5381
4. Cassio M. Oishi, Alan A. Kaptanoglu, J. Nathan Kutz and Steven L. Brunton, "Nonlinear parametric models of viscoelastic fluid flows", Royal Society Open Science, 2024.
DOI: 10.1098/rsos.240995
5. Hugo L. França, Maziyar Jalaal, and Cassio M. Oishi, "Elasto-viscoplastic spreading: From plastocapillarity to elastocapillarity", Physical Review Research, 2024.
DOI: 10.1103/PhysRevResearch.6.013226
6. Mariana B. Gonçalves, Elías Gudiño, Mauricio Maia, and Cassio M. Oishi, "Mathematical modeling for drug delivery and inflammation process: an application in macular edema", Applied Mathematical Modelling, 2023.
DOI: 10.1016/j.apm.2023.05.013
7. Hugo L. França and Cassio M. Oishi, "A machine learning strategy for computing interface curvature in Front-Tracking methods", Journal of Computational Physics, 2022.
DOI: 10.1016/j.jcp.2021.110860
8. Hugo L. França, Cassio M. Oishi and Roney L. Thompson, "Numerical investigation of shear-thinning and viscoelastic binary droplet collision", Journal of Non-Newtonian Fluid Mechanics, 2022.
DOI: 10.1016/j.jnnfm.2022.104750
9. Fabio Amaral, Wallace Casaca, Cassio M. Oishi and José A. Cuminato, "Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil", Sensors, 2021.
DOI: 10.3390/s21020540
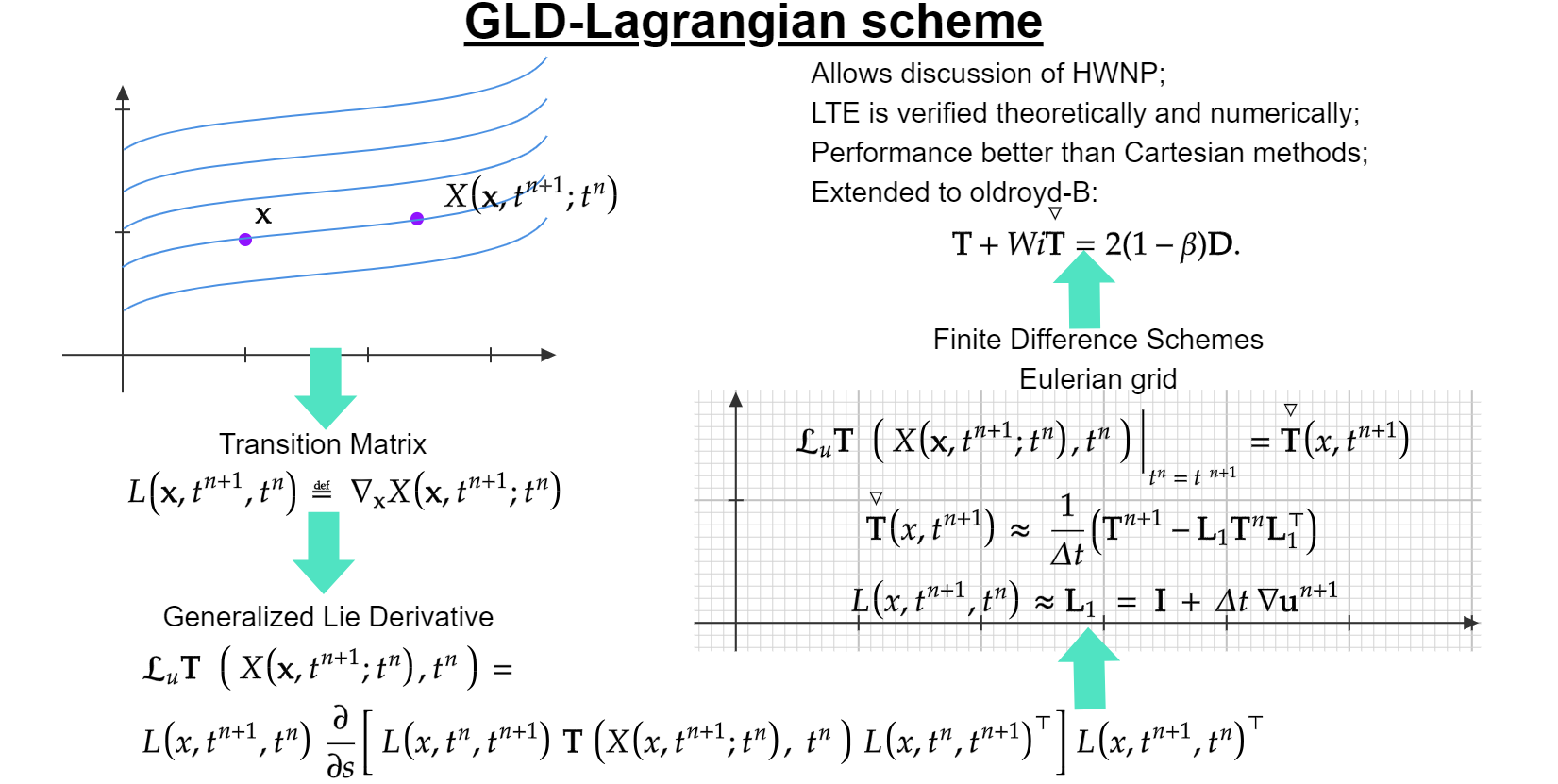
10. Jonathan D. Evans, Hugo L. França, Irineu L. Palhares Junior and Cassio M. Oishi, "Testing viscoelastic numerical schemes using the Oldroyd-B fluid in Newtonian kinematics", Applied Mathematics and Computation, 2020.
DOI: 10.1016/j.amc.2020.125106